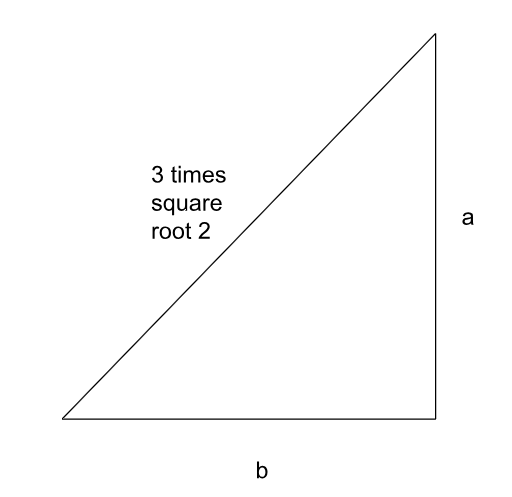
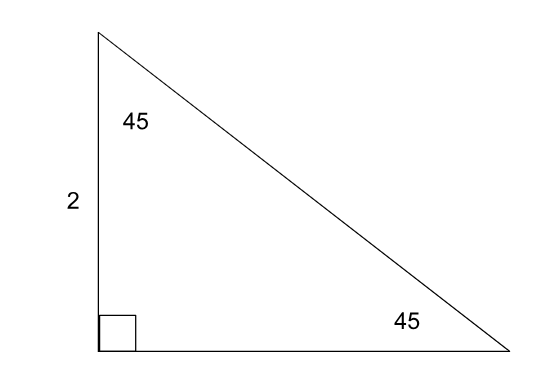
Special Right Triangles - 45°-45°-90°
Determine the missing side lengths in the special right triangles below (both are 45-45-90s).
Special Right Triangles - 30°-60°-90°
Find the missing sides in the triangles below:
Equilateral Triangle Area
Find the area of the equilateral triangle below:
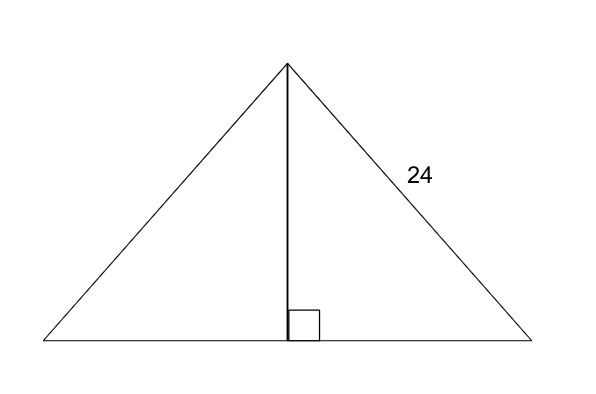
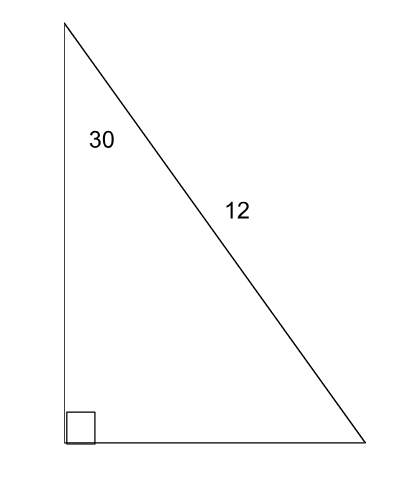
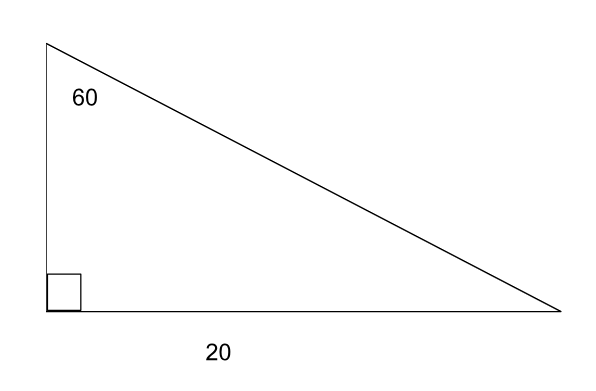
Pythagorean Theorem
-
Find the missing side in the triangle below:
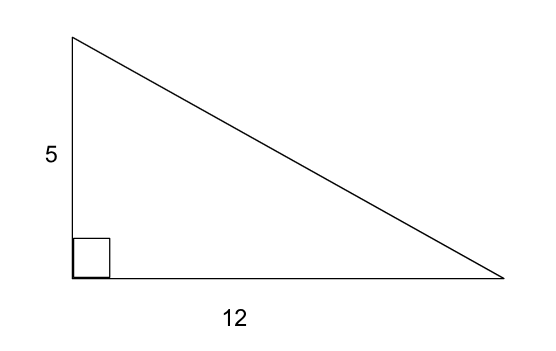
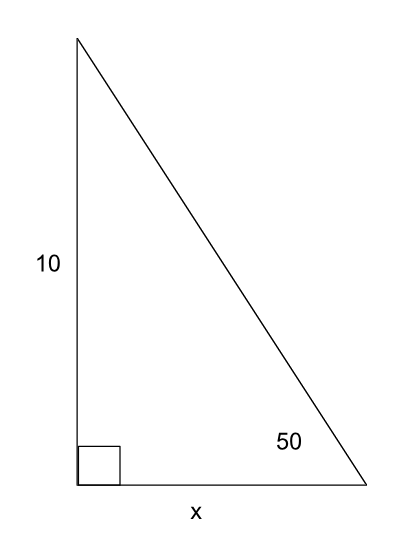
-
Find the missing side in the triangle below. Round to the nearest tenth.
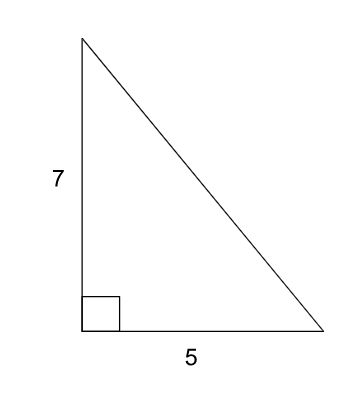
Sine, Cosine, and Tangent
-
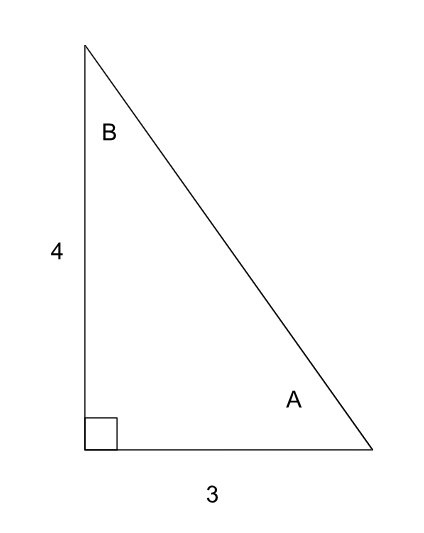
Find the sine, cosine, and tangent of angle A and B in the triangle below.
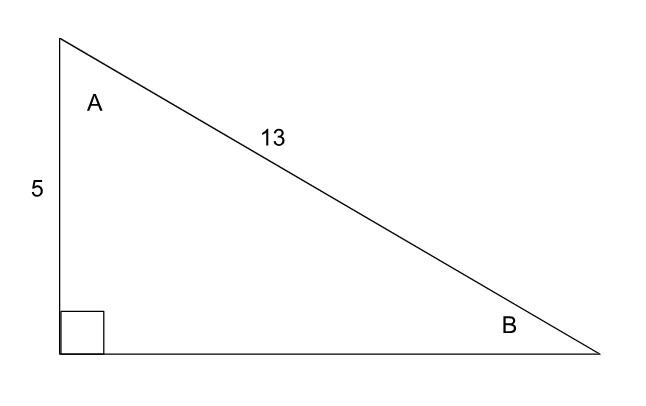
-
Find the sine, cosine, and tangent of angle A and B in the triangle below.
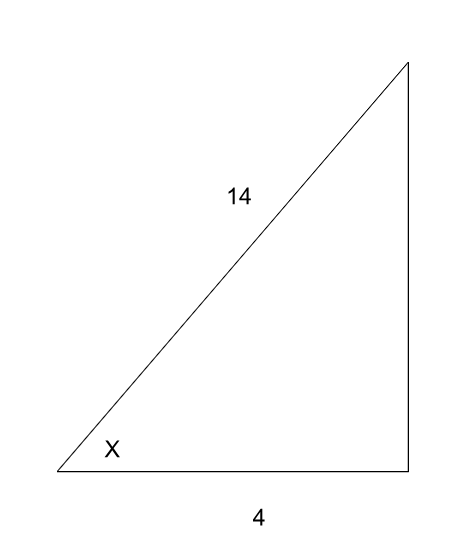
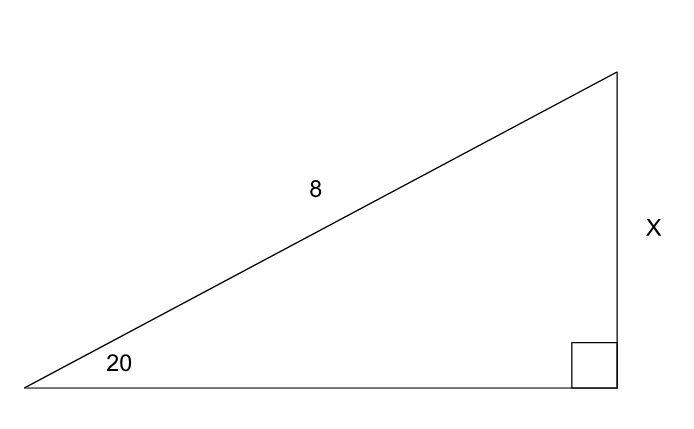
Solve for x in Right Triangles
Solve for x in the right triangles below. All angles are measured in degrees. Round to the nearest tenth.
Triangle Word Problem 1
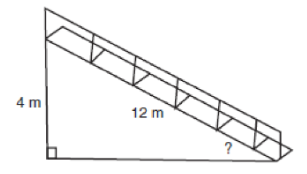
Bleachers in a stadium are 4 meters tall and have a length of 12 meters, as shown in the diagram. Calculate the measure of the angle formed by the bleachers and the ground. Round your answer to the nearest tenth.
Triangle Word Problem 2
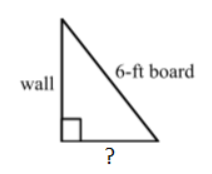
During the construction of a house, a 6-foot-long board is used to support a wall. The board touches the ground at a 67° angle. How far is the base of the wall from the bottom end of the board? Use the diagram below to help you.
More Trig Ratios
Based on the figure below, circle all TRUE equations (like a boss).
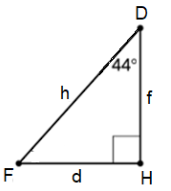
- cos(44) = d/h
- cos(46) = d/h
- sin(44) = d/h
- tan(46) = d/f
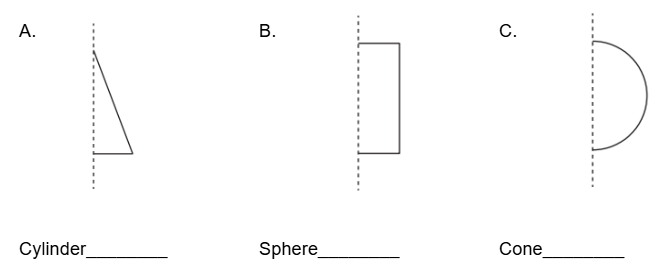
Solid Geometry Rotations
Match the two-dimensional figure and axis of rotation with the solid of rotation that can be formed by rotating the figure using that axis.
Prism Volume 1
A rectangular prism has a base with a length of 4 cm and a width of 2 cm. The prism has a height of 11 cm. What is the volume of the prism?
Cylinder Volume 1
Find the volume of a cylinder with a diameter of 10 cm and a height of 8 cm. Give your answer in terms of 𝝅 and round to the nearest tenth
Triangular Prism
Find the volume of the triangular prism below:
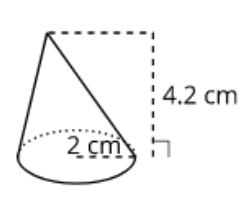
Cone Volume 1
Find the volume of the cone pictured below:
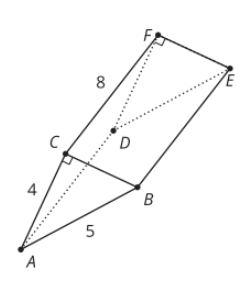
Similar Triangles 1
Consider the triangle pictured below:
Answer the following questions:
- Why are the two triangles are similar?
- What is a ratio that is equivalent to x/y?
- Given s = 15, what is the value of q?
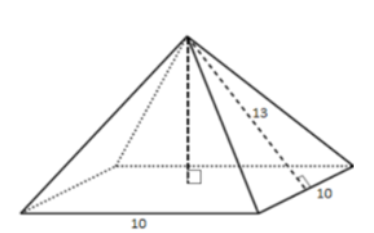
Pyramid Volume 1
A right pyramid (pictured below) has a square base with sides of length 10 units. Each segment connecting the apex to a midpoint of a side of the base has length 13 units. What is the volume of the pyramid?
Shape Formed 1
What shape is formed when you slice ...
| Circle | Rectangle | Square | Triangle | |
| a cube parallel to the base | ||||
| A cone perpendicular to the base, passing through the apex | ||||
| a cylinder perpendicular to the base | ||||
| a sphere in any direction |
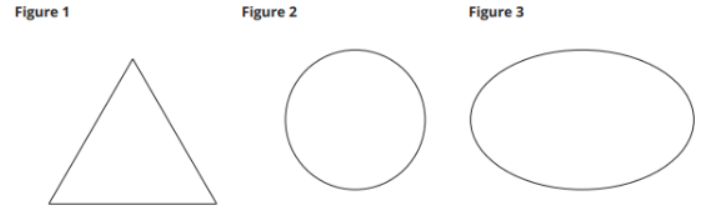
3 Cross Sections
Imagine an upright cone with its base resting on your horizontal desk. Match each plane with the image of the cross section formed by intersecting the plane with the cone.
- Parallel to the base
- Perpendicular to the base, through the cones top most point
- Diagonal
- Figure 1
- Figure 2
- Figure 3
Pyramid Volume 2
The volume of a pyramid is 50 cubic units. The base is a square with side lengths measuring 5 units. What is the height of the pyramid?
Volume Dilation 1
A solid with volume 8 cubic units is dilated by a scale factor of k to obtain a solid with a volume of 216 cubic units. Find the value of k that was used to dilate the solid.
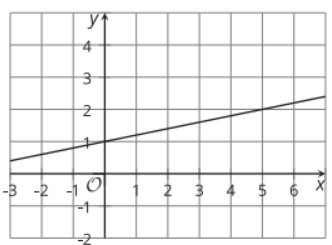
Parallel, Perpendicular, or Neither
For each equation, is the graph of the equation parallel to the line shown, perpendicular to the line shown, or neither?
- y = 0.2x
- y = −2x + 1
- y = 5x - 2
- (y - 3) = -5(x - 4)
- (y - 1) = 2(x - 3)
- 5x + y = 3
Circle Equations 1
The image shows the graph of the circle given by the equation (x - 2)2 + (y - 1)2 = 25. For each point, determine if it is on the circle or not.
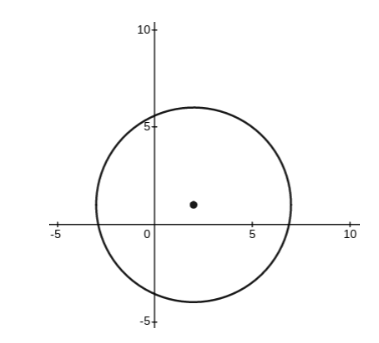
- (4, 0)
- (−3, 3)
- (−2, −2)
Circle Equations 2
Write the equation of a circle with a center of (−3, 2) and a radius of 6.
Circle Equations 3
Match each equation with it's description.
- A circle centered at (0, -4) with a radius of 3
- A circle centered at (1, -4) with a radius of √3
- A circle centered at (1, 4) with a radius of √3
- A circle centered at (1, 0) with a radius of 3
- A circle centered at (1, −4) and a radius of 3
- (x - 1)2 + y2 = 9
- x2 + (y + 4)2 = 9
- (x - 1)2 + (y - 4)2 = 3
- (x - 1)2 + (y + 4)2 = 9
- (x - 1)2 + (y + 4)2 = 3
Transformations 1
Use the diagram to answer parts a through c.
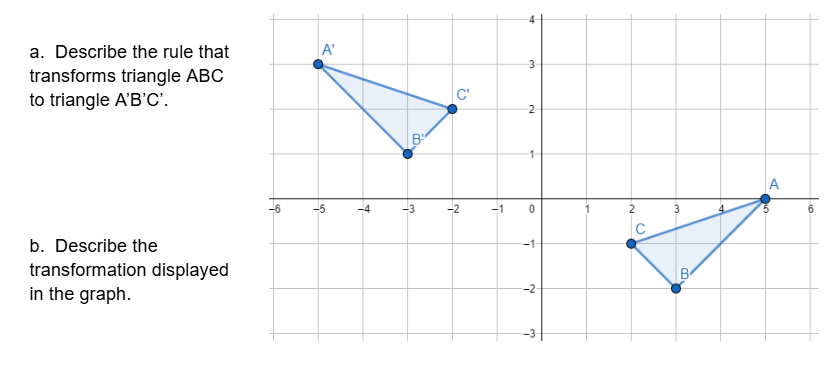
c. How is triangle ABC related to triangle A'B'C'?
- Triangle A'B'C' is congruent to triangle ABC.
- Triangle A'B'C' is similar to triangle ABC, but not congruent
- Triangle A'B'C' is neither similar nor congruent to triangle ABC
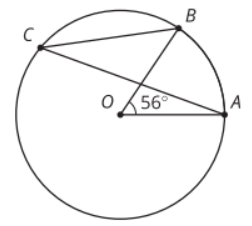
Advanced Circles 1
The measure of angle AOB is 56 degrees. What is the measure of angle ACB?
Advanced Circles 2
The images show a quadrilateral circumscribed in a circle. Highlight the arc from S to Q passing through P. Then, find the measures of:
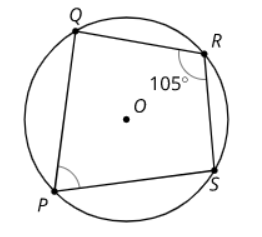
- the arc you highlighted
- the other arc from S to Q
- angle SPQ
Advanced Circles 3
The picture shows a quadrilateral with a circumscribed circle. What is the value of ⍺+𝜷? Explain or show your reasoning.
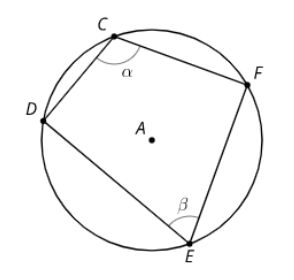
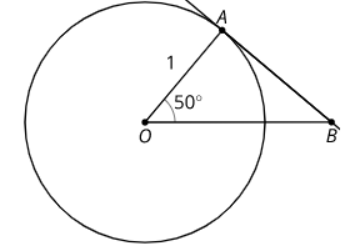
Advanced Circles 4
Line AB is tangent to the circle centered at O. Find the measure of angle B.